Physics
Spherical, Cylindrical, Plane-Wave Sources
Most are familiar with the properties of one type of sound source – the spherical-wave source – because virtually every loudspeaker is an example of this type. But there are two other types: the cylindrical-wave source, and the plane-wave source. These sources are named for the shapes of the sound waves they produce, and each has significantly different properties:
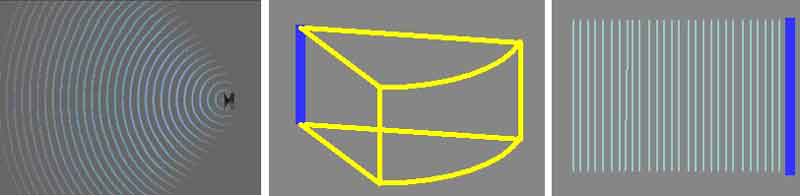
- A spherical-wave source is shaped like a typical loudspeaker. Spherical sound waves expand in three dimensions – like an expanding sphere: out, left and right, and up and down.
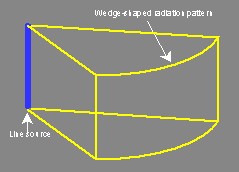
- A cylindrical-wave source is shaped like a line. To produce cylindrical waves at musical frequencies the source must be high, about six feet (two meters), or higher. Cylindrical waves expand in two dimensions only – out and to the sides but not up or down (assuming the source is oriented vertically, like a flagpole).
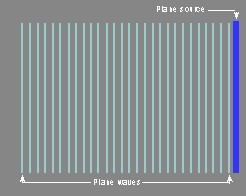
- A source capable of producing plane waves is itself planar, or sheet-like, in shape. To produce plane waves at musical frequencies the plane-wave source must be large, about six feet square (two meters square), or larger. Plane waves travel in only one direction, or dimension: out, but not to the sides or up and down.
In addition to the different shaped waves produced by the three different source types, waves from spherical, cylindrical, and plane-wave sources also differ in the rate at which sound diminishes with distance from a source.
- Spherical waves retain only one-fourth of their sound intensity with each doubling of distance from the source. For example, if the sound intensity is 100 units at 10 feet from the source, it will be only 25 units at 20 feet, about 6 units at forty feet, and so on. We hear this as a dramatic reduction in sound level with distance from the source. Conversely, if we approach a spherical-wave source that is at a comfortable volume level, it soon reaches a level that is uncomfortably loud. It is this fundamental property that makes spherical-wave sources unsuitable for the challenge of creating sound that can serve both the musician and the audience at the same time without being too loud or soft for either.
- Cylindrical waves do not lose intensity with distance as fast as spherical waves. They lose only half their intensity with each doubling of distance. Thus if the sound intensity is 100 units at 10 feet, it will be 50 units at 20 feet, 25 units at forty feet, and so on. We hear this reduction of level with distance as modest in comparison with the spherical-wave source. With such a source, if we set the correct level in the audience and then move closer, we hear the level as increasing only modestly. In fact, you can walk right up next to a cylindrical-wave source and never have the feeling that it is too loud. These properties will turn out to be of major importance to the problems of amplified music.
- Plane waves theoretically lose no sound intensity with distance. Thus if the sound intensity is 100 units at 10 feet from the source, it will be still be 100 units at 20 feet, 100 units at forty feet, and so on. From this perspective, plane waves would be ideal for music performance because musicians and audience would get the same sound level.
For the reader interested in understanding the underlying physics of these differences, imagine a sound-intensity-meter in front of each kind of source, at a distance of say ten feet. Furthermore, imagine that at this distance, each source produces the same level. Now, consider a small area of the sound wave at the location of the meter.
- As the spherical wave spreads out, the wave must expand over the surface of a sphere. When the sphere doubles in diameter, the small area of the sound wave must expand over a proportionately larger area at the doubled distance. As a result the intensity of the original area of sound wave diminishes. Since the area of a sphere increases as the square of the radius, increasing the distance from the source by a factor of two (doubling the distance and therefore the radius) means reducing the sound intensity by a factor of four (two squared).
- As the cylindrical wave spreads out, the wave must expand over the surface of a cylinder. When the cylinder doubles in diameter, the small area of the sound wave at the closer distance must spread over a proportionately larger area at the doubled distance. As a result the intensity of the original area of sound wave is reduced. Since the area of a cylinder increases proportionately with only the radius (rather than as the square of the radius), increasing the distance from the source by a factor of two (doubling the radius) means reducing the sound intensity by only a factor of two.
- As the plane wave progresses, the wave does not expand. When the wave reaches a distance that’s double the original, the small area of the sound wave at the closer distance hasn’t spread at all, and as a result the intensity of the original piece of sound wave is the same.